Chapter IV: Mathematics | The Philosophy Of Science by Steven Gussman [1st Edition]

        “[The universe] cannot be read until we have learnt the language and become familiar with the

        characters in which it is written. It is written in mathematical language, and the letters are

        triangles, circles and other geometrical figures, without which means it is humanly impossible

        to comprehend a single world.”

        – Galileo Galilei (1623)^I

        I want to put forth a word of caution about the present "Mathematics" chapter, as well as the following "Computation" chapter: they are the most technical in this book.  They represent a technical survey that runs that gamut from what you would have learned in K-12 school (though perhaps could better understand and appreciate as an adult), to some of what university undergraduates might learn.  As a result, I certainly don't expect most people to be able to keep up with everything in these sections, given no prior training.  I do not want this material to scare the reader off, nor bore them if they are less interested in (or less able to grasp) the technical details.  At the same time, I do not want to discourage the uncertain reader from experiencing such formalisms: my hope is that you will read these chapters without worrying too much about how well you can understand or follow along with the details (there will be no test at the end!).  Expose yourself to it, is all that I ask.   If nothing else, the reader should find value in the philosophy of mathematics between the technical notes.  That said, if one finds oneself confused, intimidated, or bored, I do ask that you simply skip these technical sections rather than the entire rest of this book, which is largely prose: the philosophical arguments are both more important to the thesis of this book, and more easy to grasp (even if they may be revelatory once grasped).   Even void of the technical formalisms, one will benefit much from understanding the basic philosophy of science, and it should help one make decisions on what they believe in the future.   These chapters are also some of the longest singular sections in this book, which I lament because, again, technical details are not the main point in this work.   That said, it is important to me to expose the reader to them, and to provide a reference (of tools) for anyone who might want to attempt a quantitative calculation to test a scientific hypothesis they may have.   Many authors pride themselves on including no technical content (such as economist Thomas Sowell's Basic Economics), or (slightly better) they relegate all technical material to a mathematical appendix at the end (such as physicist Steven Weinberg's To Explain The World).   I think that this serves the worst intuitions of the lay-reader, in letting them take no look at such daunting material.   I prefer to give a nice little survey that doesn't go too deep, but doesn't shy away from showing the real content.   I didn't want to hide the important part of the field of philosophy of science (an important tool for how to think about the world ) that is mathematization.   Without further ado, I have blocked out the technical sections of this book between these section-separation symbols: 〰〰, such that one may navigate between technical mathematics and philosophical prose for oneself.

        Mathematics is the extension of formal logic to deal with quantities.  In fact, logic and mathematics are essentially unified in the simplest version of a number system: binary (or base-two).   It is our strictest, most deductive philosophy.   The Indo-Arabic symbols we happen to use (and not all cultures who made discoveries in math always used that notation) is quite good for the job, but it is not to be confused with the content of the subject itself.   Mathematical laws govern the state and transformations of quantities whether or not we know about it, write about it, or use any particular written symbology to express them.  One can see this when they consider that the symbols used in "one and one makes two" and "1 + 1 = 2" are entirely different, yet they communicate the same undeniable fact that if you have an apple and I give you another, you will now have two apples.   Mathematics is discovered, not invented (even if it takes particularly inventive people to uncover these truths—and it certainly does).   As Galileo said, mathematics is the language of the universe.  Mathematics is how we formalize, or make quantitative our qualitative knowledge of the world.

        There are a few particularly special, simple numbers: -1, 0, 1, and 2.  The number one is special because it is the introduction of quantity at all and because it signifies unity: in some sense there can only be one thing—one cosmos—even if it is useful to cut it up, isolate its parts, and reduce it into understandable chunks.   Zero is special because it allows us to formally treat situations where we have nothing (among other things, opening the door to push past into the negative realm).   This often gives us a natural origin to work about.   Negative-one is special because it allows us to think about having less than zero of something—a debt (which also unifies addition and subtraction into generalized summation: the addition of a negative number is subtraction, and the subtraction of a negative number is addition).   Neither of these two were obvious to ancient peoples and constituted ground-breaking discoveries, though we take them for granted today.   And finally, two is special because it introduces the concept of multiple things—such counting (or quantification) is ultimately the point of arithmetic.

        Units are important because they bring our mathematics back in contact with the physical world; it is through units that mathematics truly becomes the language of our universe.  Units are simply a recognition of basic spatial relativity (not to be confused with Einsteinian relativity theory, which we will discuss in the “Cosmology”, “Astronomy”, and “Physics” chapters), which is the recognition that, in infinite space, there is no absolute scale.   If the universe were three-dimensional and consisted of one object, say a perfect cube floating in space, one could have nothing to say about its size—the concept itself would be meaningless, and its invocation could encode no information.   This is because the only lengths that exist in this universe (all 12 of the cube's edges) are exactly the same size; as a result, the only areas that exist in this universe (all six of the cube's faces) are exactly the same size; and finally, the only volume that exists in this entire universe is the one of the cube.   The cube has edges, surface areas, and a volume, and one could speak about the equations that relate them to each other (one could say, for example, that the volume is the cube—or raising to the third power—of the edge length, and the area is the square—raising to the second power—of the edge length), but one could not actually specify what any of these numerical quantities were; they would have to be content to set the edge length as 1 edge-unit, the surface areas as 1 edge-unit², and the volume as 1 edge-unit³.  And with nothing to compare this to, it wouldn't matter!   But now imagine we introduce a second cube in the universe, whose edge-lengths are half the size of the one we already have.   Now we have a real, useful unit!   We can take either cube's side length as our unit, and describe the other in terms of it.  If we take the smaller cube's edge-length to be our unit of length and call it a “blip”, then we can describe the larger cube as having an edge-length of 2 blips, an area of 2² = 4 square-blips (or blips²), and a volume of 2³ = 8 cubic-blips (or blips³).  If this seems strange, realize that it is exactly the case in our more complex universe!  Though many exist, modern scientists have agreed upon a standard set of units for each variable, known as the SI units.  The SI unit for length is the meter [m] (square-brackets in this context denote the symbolic abbreviation used for a given unit); to express a length of eight meters, one may simply write: 8 m.  But what is a meter? One might absent-mindedly assume that the meter really has some essential lengthiness to it, because we tend to treat it that way.  But it is actually just a particularly useful length (for human-scale applications), which we are (now) particularly able to precisely measure.  While the actual length of a meter hasn't changed much (which would defeat the purpose), its precision has because we have come up with more precise definitions for it so that it may remain useful in more extreme scenarios (such as on very small scales).^II  It was originally defined as a particular fraction of one of Earth's longitudinal lines but has most recently been redefined as the length a particular frequency of light (emitted from a particular chemical element) travels in a particular length of time (which exploits our highly precise measurements of a fundamental physical constant: the speed of light).^II  In fact, a standard meter, a physical bar of that length (going by a slightly older definition of the meter) exists in France, and when we say that something is two meters long, we are really saying that its length is twice that of this French bar.^II  The same is true for every variable's units (from lengths of space, to durations of time, and even the magnitudes of masses).  A unit is really a ratio of different quantities in disguise (implying, perhaps, that only such dimensionless ratios exist, at bottom, mathematics being the precision-quantification of relationships).^III

        Physics may be able to essentially bring back some semblance of absolutism: if a given length is found to be truly the smallest physical length (some physicists attempt to approximate such a quantity with what they call the Planck length), then even though one is still dealing in a relative ratio of Plank lengths when using it as a unit, it would indeed be the smallest unit, with all other measurements necessarily an integer multiple of these (which has implications for both accuracy and precision).  Indeed, the strange idea at the heart of quantum physics (our lowest-level theory of nature), is that at least some quantities are qunatized, or made up of the integer sum of smallest-possible discrete parts, rather than the integration over infinitely many infinitesimal parts which characterizes calculus (but more on quantum physics in the “Physics” chapter).

〰〰

        Sets are groups of different kinds of numbers, as some numbers share more in common than others.  Among the most famous (followed by the symbol that represents their set) are the integers (ℤ), rational numbers (ℚ), irrational numbers (ℚ'), real numbers (ℝ), prime numbers (P), and the complex numbers (ℂ).  The integers are the first numbers we are introduced to, and we are introduced to them as whole numbers because they have no fractional part.  As far as we know, there are infinitely many of them, and they are each a distance of one from each other on the number line (or, in other words, they are all multiples of one).  Some examples of integers are: -3, -2, -1, 0, 1, 2, and 3.  When one is talking about quantifying entire objects, such as the answers to questions like, “How many people have died in the year 2021,” one uses integers.  Real numbers include fractional numbers (as well as integers), which helps us to quantify the fact that sometimes objects break apart or come together (or otherwise that most units are made from a conglomeration of smaller units).  There seem to be not only infinitely many of these in either direction on the number line, but in fact infinitely many of them in-between any other two real numbers you may choose.  This is important because just as any numbers at all (say, integers) introduce the concept of accuracy (how close to the real empirical answer one is), real numbers expands the concept of precision (how many “places”, including out beyond the decimal point one's quantification goes, with the leftmost digit known as the most significant digit and the right-most known as the least significant digit because of the diminishing contribution each “place” represents in a number).  Some examples of real numbers include ±π, ±2.0, ±1.154, and ±½ (± means “plus or minus”; either sign is okay).  Real numbers are so called because in real-world situations, one often has to deal with partial numbers due both to the reality of most units being separable or composite, and due to uncertainty and error in calculations: one uses real numbers when dealing with money, for example, because “dollars” are a composite unit of many “penny” units (one could alternatively use only integer amounts of pennies, but it is not practical).  One subset of real numbers are the rational numbers—these are often introduced to us as fractions because they may be expressed as simple integer-ratios, or divisor-dividend pairs.  This set inherits their infinite status from that of the integers they're made from.  Some examples of rational numbers are ±1/3, ±½, ±1/1, and ±0/1.  Another set is irrational numbers, those fractional numbers which cannot be expressed in this simple way, and instead require decimal notation—sometimes, these numbers appear to be impossible to write down precisely, because they seem to have infinitely many decimal-place values (the potential for patterns in which remains an open mystery in mathematics, today).  One example of an irrational number would be ±26.31546 (with the closest rational number being 52 / 2 ≈ 26).  Perhaps the most famous irrational number is π ≈ 3.14159.., which is the ratio of any circle's circumference to its diameter (as mentioned in a prior footnote).  These previous two sets would appear to be so-named because the ancients thought that mathematical elegance would require the beauty of the rational numbers and preclude the strangeness of the irrational numbers; as it stands, rational numbers do remind us of the elegance of mathematics, whereas irrational numbers remind us of the deep mysteries lurking even in the most mundane places.^IV  Finally, (though there exist more, and likely even some undiscovered sets), we have the prime numbers: these are rational numbers whose only factors are themselves and one (in other words, numbers for whom the only way to express them as a ratio is x / 1, where x is the prime number).  Some examples of primes include ±13 and ±3 (because, for example, the only two numbers one may multiply together to get the product 13, are 13 and 1).  It is not known how many primes there are, nor is any great process known for finding them—the mathematician's obsession with the quest for a law of primes is perhaps what explains this set's lofty name.  Finally, we will talk briefly about complex numbers which are a mix of real numbers and imaginary numbers.  It's worth dispelling a common misconception right away: the “imaginary” in the name of this set of numbers is not to be taken too seriously.  These are strange quantities, but they seem to be as real as one and two, and their traditional name comes from Descartes, who thought their existence would be disproven.^V  This will make more sense later when we've taken a look at exponents and roots, but suffice it to say that when you square a number, you multiply it by itself; and when you take the square root of a number, you ask what number multiplied by itself could produce the original number (that is, these functions are inverses of each other—they undo each other).  The interesting thing about square roots is that because multiplying two negative numbers (or, obviously, two positive numbers) together produces a positive number, each number has two square roots—one positive and one negative.  But what happens when one takes the square root of a negative number—in the simplest case, -1? For a long time, this was thought to be undefined and illegal because nothing multiplied by itself would appear to yield a negative number.  But it turns out there is such a quantity, the imaginary number denoted by i:^VI

√-1 = i ≡ i² = -1

Complex numbers merely mix real numbers with imaginary numbers, something like: 45 + 7i.  These have proven useful in the physical world, as they are integral to quantum physics (for more on this topic, see the “Physics” chapter in the “Ontology” section).

        There also exist some special values in mathematics, such as infinity (which we've mentioned before in terms of the number of numbers), a concept meant to denote a value larger than any you can name.  Many mathematicians believe that there are different sized infinities which may be compared, an answer they come to based on pure logic; for example, it would only seem logical that there are more real numbers than there are integers (despite there being infinitely many of each), because the integers are a subset of the real numbers (in other words, because there appear to be infinitely many real numbers between any two contiguous integers (but of course no integers at all between two contiguous integers).^VII  Others don't believe infinity exists at all, and some other concept (such as perhaps an incredibly large maximum value and precision limit) will ultimately replace the infinity approximation—not unlike those which exist in our computers, dependent on their hardware specifications.^VIII

        There are four main sub-fields of mathematics to familiarize oneself with: arithmetic, algebra, geometry, and calculus.  Arithmetic is the basis of mathematics (and is sometimes called counting).  It encompasses the basic laws of mathematics, such as operations and operands.  The operands are numbers (or variables holding numbers) whereas the operators represent the particular transformation being used to change a number into a new one. For example:

1 + 2 = 3

Here, 1 and 2 are the operands, addition is the operation, and the summation 3 is the yield.  Addition and subtraction (or summation, more generally) is just the linear combination of values as described earlier, identifiable by the word "and"—“100 and 5 make 105”, for example.  Multiplication is simply multiple-addition^IX and its yield is called the product: “100 times 5 is 500” (or the addition of 100 five times: 100 + 100 + 100 + 100 + 100):^X

100 × 5 = 500

Multiplication is simple, but things may get a bit more complicated if one is dealing with the multiplication of two entire expressions.  Consider the following expression:

(3x² + 4x) × (x² - 10x + 4)

How should one go about performing such a calculation?  The technique is called distribution and it simply means that you multiply each term in the first parenthetical by each term in the second parenthetical and then combine (or sum over) the answers, like so:
    (3x² × x²) + (3x² × -10x) + (3x² × 4) + (4x × x²) + (4x × -10x) + (4x × 4) =

    3x⁴ – 30x³ + 12x² +4x³ – 40x² + 16x =

    3x⁴ – 26x³ – 28x² + 16x

(Note that the product of two variables is the sum of their coefficients, or numeral multipliers, and their variable is raised to the sum of the two terms' exponents.  The last step is called simplification, in which like terms which have the same variable and exponent may be combined, as in 2x + 3x = 5x).  As subtraction is to addition, division is the inverse operation to multiplication: it is how many times a numbers goes into another number.  This means that this is the first operation we have seen that is not commutative: the order of the operands matters:

                                        100 + 5 = 5 + 100

                                        100 × 5 = 5 × 100

                                        100 ÷ 5 ≠ 5 ÷ 100

With division, the operands therefore have special names: the first is the dividend and the second is the divisor^XI (since fractions are equivalent to division as the division symbol suggests, these may also be called the numerator and denominator).  When one says 100 / 5, they are asking "how many multiples of 5 does it take to make 100"—the answer (or quotient) to which is 20:

100 / 5 = 20

Shortly, we will learn about algebra which is based on the realization that this is just a rearranged way of expressing:

5 × 20 = 100

Interestingly, it is also the case that 100 / 20 = 5, and algebra will make it more clear why this is the case.  Therefore:

x × y = z ≡ z / x = y ≡ z / y = x

Mathematics begins to graduate from mere arithmetic to algebra when we realize we can use the basic arithmetic laws to balance, rearrange, and even solve equations containing variables (following the law that any arithmetic we do to the expression on one side of the equals sign must be done to the other):

8x + 2 = 10x – 6 ≡ 4x + 1 = 5x – 3 ≡ x = 4

Here we divided both sides of the equation by 2, then added three to both sides and subtracted 4x from both sides, and finally swapped the sides such that x appears on the left out of convention, which finally solved for x (this process is called simplification because it expresses the same equation with the smallest possible numerals; the inverse is called expansion).  Note that you cannot divide by zero, the “answer” to which we denote as “undefined” or “not a number” / “NaN”.  To begin to realize why, imagine that 1 / 0 = x and then rearrange it such that 1 = 0 × x or 0 = 1 / x: there cannot be a number we could multiply by zero to get 1 (multiplication by zero always equals zero) nor a number we could divide by to get zero—even division by very larges number can only ever asymptotically approach zero without reaching it.

        Next are exponentials, wherein a base is raised to an exponent, for example:

2⁷ = 128

This is multiple-multiplication—it means you take the self-product of the base 2 for the exponent 7 terms: 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128.  When the exponent is 0, the product is always 1, regardless of the base (which will prove important when we discuss different number systems, which all share the base⁰ = 1's place, the linchpin of mathematical language).  When the exponent is 1, the answer is always the base itself (because you take the base for one term).  When the exponent is 2, this is called the square because it gives the area of a square of the base dimension.

When the exponent is 3, it is called the cube because it is the volume of a cube of the base dimension:

All together, with the example base of 3:
                                                3⁰ = 1

                                                3¹ = 3

                                                3² = 9

                                                3³ = 27

As you have already seen, exponentiation begins to shine light on geometry: the mathematical study of shapes (or the mathematical structures that may be used to describe shapes).  This is because the area (two-dimensional), volume (three-dimensional), hyper-volume (four-dimensional), and generally, n-volume (n-dimensional) of shapes are calculated by variations on the simple equation in which the area of a rectangle is equal to the base times the height:

A_Rectangle = bh

Therefore in the special case of the square, where the base equals the height—which we'll call simply the length, ℒ, the area is:

                                            A_Square = ℒ × ℒ

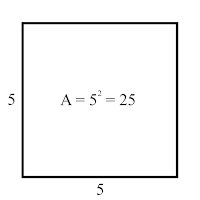
                                            A_Square = ℒ ²

                               

Now one can derive the area of a triangle by imagining a rectangle created by fitting another two-dimensionally-mirrored triangle to the other; this makes it clear that the area of a triangle is merely half of the area of the rectangle constructed in this way:
                                            A_Triangle = ½ × bh
                                            A_Triangle = bh / 2

                                 

Similarly, one realizes the area of an equilateral triangle (a triangle whose sides are all of equal length, and whose angles are consequently each 60°—as all three angles in any triangle must sum up to 180°) is half the area of a square of the same edge-length:

A_{Equilateral-Triangle} = ℒ ² / 2

Many nice, hard-edged Euclidean shapes' areas may have their areas more-or-less easily calculated by breaking them up into smaller rectangles or triangles (known as tessellation) whose areas you can sum for the total.  The following is an example of how a trapezoid of known bases and height can be broken down into three triangles, the sum of whose areas is the total trapezoidal area:

Curves complicate things, but that perfect curved shape, the circle, is amenable to a simple area calculation: the product of 2, the geometric constant π, and the square of the circle's radius (half its diameter), r²:

A_Circle = 2πr²

Recognize that the r² is the area of a square whose lengths are equal to half of the diameter of the circle (meaning such a square is smaller than the circle); 2π must then encode the information about the curved regions surrounding this square, making it into a circle.

Similar reasoning may reveal how to calculate the volumes of regular three-dimensional shapes as well:^XII

V_{Rectangular-Prism} = bhd

V_Cube = ℒ ³

V_{Rectangular-Pyramid} = bhd / 3

V_Cylinder = πr²h

V_Cone = πr² (h/3)

V_Sphere = (4/3)πr³

From here, one can even generalize to arbitrary numbers of dimensions, but that is beyond the scope of this book (and not commonly used, as we appear to occupy a three-dimensional spatial world).

        Now, there are two related operations left to discuss here, one for retrieving the base of a number given an exponent, and one for retrieving the exponent given the base.  The first is the root, which provides an exponent and returns the necessary base to get the number in question:

²√25 = √25 = 5

because 5² = 25.  Here, we can also see that the implicit radical symbol (with no provided exponent) is assumed to be two (the square root).  Taking the root with exponent 3 is similarly called the cube root.  One uses logarithms to provide a base and get the back the concomitant exponent:

log₅(25) = 2

because one must raise the base 5 to the exponent 2 to get 25.  Therefore, generally:

a^x = b ≡ ^x√b = a ≡ log_a(b) = x

Nifty!  In fact, there is technically no difference at all between exponentials and root operations: the square root of a number is the same as taking a number to the ½ power:

^x√a = a^(1/x)

and of course, vice versa:

b^y = ^(1/y)√b

Thus it is clear that exponential and root functions are one in the same, with logarithms as their inverse function.  In fact, there exists a function which is its own inverse function: to take the inverse of any number, raise it to the -1 power:

                                            x^-1 = 1 / x

                                            (1/x)^-1 = x

In fact, whenever an exponent is negative, you can treat it as a positive exponent with that term in the denominator of a fraction:

x^-a = 1 / x^a

        Now that we have seen basic arithmetic, we should go over the order-of-operations, or, the order in which to perform operations which are written out in a single line.  The acronym for this is PEMDAS.  It means that in order of descending precedence, one should calculate parentheticals, then exponents, then multiplication and division according to which comes first, and finally addition and subtraction according to which comes first.  For example, take the following expression:
                                    (5 + 6) + 2 - 1 × 10² - 3 / 6

A naive left-to-right reading of this might cause one to perform the following calculation:

                                    11 + 2 - 1 × 10² - 3 / 6

                                    13 - 1 × 10² - 3 / 6

                                    12 × 10² - 3 / 6

                                    120² - 3 / 6

                                    14,400 - 3 / 6

                                    14, 397 / 6

                                    2,399.5

But that would be wrong!  The following steps should instead be followed, according to the order-of-operations (PEMDAS):
                                    11 + 2 – 1 × 100 - 3 / 6
                                    11 + 2 - 100 - 0.5

                                    13 - 99.5
                                    -86.5

Very different outcomes, indeed.  Be mindful!

        Now we may return to geometry to explore a few more fundamentals.  As a short introduction to the important field of trigonometry (the geometry of triangles), we will look at the Pythagorean theorem as well as the trigonometric functions.  The ancient Greek Pythagoreans (and, it appears, some before them)^XIII discovered a formula for the sizes of the legs of a right-triangle (a triangle which has a right-angle).  That is that the square of the length of the hypotenuse (the longest leg which is across from the right-angle) is equivalent to the sum of the squares of the other two leg lengths:

a² + b² = c²

This means that if you know the length of any two legs of any right-triangle, you can deduce the final leg:

a² + b² = c² ≡ c = √(a² + b²) ≡ a = √(c² - b²) ≡ b = √(c² – a²)

A nice feature of triangles which makes the Pythagorean theorem even more powerful is the fact that one may always divide a triangle into two right triangles.  In other cases, one may find a third leg length of any right triangle for which two leg lengths and one of the two remaining angles is known.^XIV  First, we will name the legs, based on the known non-right-angle (one of the two which subtends the hypotenuse):

As you can see, you have the hypotenuse itself (the longest leg), the known angle (which is between the hypotenuse and one of the remaining two legs), then you have the adjacent leg (the one other than the hypotenuse that the known angle is connected to), and finally, the opposite leg (that is, opposite and away from the known angle).  If you know any two of these legs, you can use the normal functions: sin(θ), cos(θ), or tan(θ) to calculate the other.  There is much more to these functions (and there are more trigonometric functions) than the scope of our discussion here, but one can remember how to use them in this context with the mnemonic device, “SOH CAH TOA” (where “S” means sine, “C” means cosine, “T” means tangent, “O” means opposite leg, “A” means adjacent leg, and “H” means hypotenuse).  If you know the opposite and hypotenuse legs, then you say, “SOH,” and calculate the adjacent leg length thus:

A = sin(O / H)

(the “S” means to use the sine function, and the “OH” means to pass in O / H).  If you know adjacent and hypotenuse legs, then you say, “CAH,” and calculate:

O = cos(A / H)

(the “C” means to use the cosine function, and the “AH” means to pass in A / H).  Finally, if you know the opposite and adjacent leg lengths, you say, “TOA,” and calculate:

H = tan(O / A)

(the “T” means to use the tangent function, and the “OA” means to pass in O / A).  There are also inverse trig functions which do the opposite: given two leg lengths, one may retrieve the angle, theta:^XIV
                                        θ = sin^-1(O / H)

                                        θ = cos^-1(A / H)

                                        θ = tan^-1(O / A)

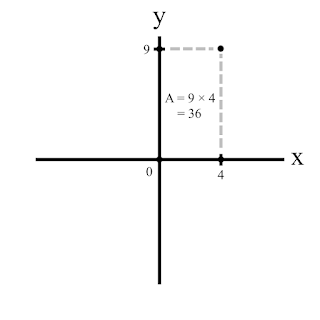
        Next up are coordinate systems (ways of dealing with the empty space geometric objects exist inside of): the Cartesian coordinate system and the polar coordinate system.  In some sense, we have already explored the first when we looked at how to calculate shapes' areas and volumes: the Cartesian coordinate system takes some set of n perpendicular or orthogonal (at right-angles) number lines to be the basis dimensions (conventionally, these are left-right and up-down—and forward-back, if you want a third dimension) and places the origin where they all meet at 0 on each number line.

Here, any position or point (points are zero-dimensional geometric objects—essentially locations in space) may be denoted by the values of its location on each axis (conventionally separated by commas and contained in parentheses):

Then a line may be drawn between any two points, and the equation representing a line running in this direction (an equation whose solution-set is the set of all infinitely many points along that line) will take the simple form:

y = mx + b

where m is the slope (or steepness) of the line and b is the y-intercept (where on the y-axis the line intersects with that dimension), and of course (x, y) represent the infinitely many point-pairs along the line:

In turn, edges may be combined to form shapes, such as rectangles!  Imagine that the shapes we looked at earlier existed in a Cartesian space where their corners were specified point-locations, with edges that connected these (the difference between the points giving the edge lengths).  Here again, it is easy to see how to calculate the rectangle's area:

Or otherwise, equations whose solutions are the infinitely many points on curved perimeters (or surfaces, in three dimensions) may be found, such as that for a circle:

x² + y² = r

The polar coordinate system, on the other hand, deals with angles instead of with perpendicular dimensions: instead of x and y, the basis for the polar coordinate system is a singular axis r (equivalent to x in the Cartesian setup) and the angle from r, θ:

Whereas Cartesian coordinates are well setup to deal with hard-edged Euclidean shapes, polar coordinates are better suited to curves such as circles.  Defining the equation for a square in the polar dialect would be stilted and ugly, but the circle comes from setting the radius r constant and varying only the angle θ—each (r, θ) pair is then just the infinitely many points on a circle of radius r (when the radius is set to 1, it is known as the unit circle).

        The Cartesian coordinate system and the polar coordinate system are just two ways of looking at the same mathematical space, and so one may follow mathematical laws (which describe a triangle whose adjacent leg is the Cartesian x-axis, whose opposite leg is the Cartesian y-axis, and in which r is the hypotenuse) to translate between these two dialects of the single mathematical language:^XV

    

                                        r = √(x² + y²)

                                        θ = tan^-1(y / x)

                                        x = rcos(θ)

                                        y = rsin(θ)

Indeed, because some problems (or even parts of problems) are easier to solve in one or the other system, it is good to know how to change lenses by transforming one into the other!

        So far, we have largely taken for granted that we are working in a base-10 (or decimal) number system.  All of the same laws of arithmetic and geometry hold across any number system, these just deal with the meaning of our symbolic language used to describe universal mathematics.  To begin, let's take a closer look at what a base-10 number system is.  Consider the following number: 1,452.8701₁₀.^XVI  How do you know how to read it?  Well, you learned what the number places mean: in this case, you have the thousands place, followed by the hundreds place, tens place, ones place, tenths place, hundredths place, thousandths place, and finally the ten-thousandths place, all coming together to give you “one-thousand, four-hundred, fifty-two; and eight-tenths, seven-hundredths, and one-ten-thousandth.”  Here is the number with its “places” explicitly above each value in gray:
                1,000    100    10    1    0.1    0.01    0.001    0.0001

                    1         4       5     2     8        7           0           1

One may not realize they are doing it, because it is essentially rote at this point, but one is really summing over the products of each single-digit value and the “place” it occupies: the written number is then (1 × 1,000) + (4 × 100) + (5 × 10) + (2 × 1) + (8 × 0.1) + (7 × 0.01) + (0 × 0.001) + (1 × 0.0001) = 1,452.8701₁₀.  What do you notice about the “place” values?  Each is a multiple of ten!  That is precisely what it means to say that this is a base-10 number.

        At this point, we must take a brief detour to talk about orders of magnitude.  Orders of magnitude are technically number-system dependent, but for the same reason that base-10 is usually the implicit number system, an order of magnitude is usually defined as a factor of ten: this means that the number 100 is an order of magnitude larger than the number 10, and that the number 25 is three orders-of-magnitude smaller than the number 25,000.  But typically, when we are talking about orders of magnitude, we actually don't care about the specific values of each digit because in the context of differences in orders-of-magnitude, they are not terribly significant (see the “Approximation” chapter for more on this topic).  As mentioned earlier, a multi-digit number has a most-significant digit (the leftmost) and a least-significant digit (the right-most), because from left-to-right, each digit contributes less to the total magnitude of the number (in the above example of 1,452.8701, the first 1 is the most-significant digit because it contributes 1,000 to the total number, whereas the last 1 is the least-significant digit because it only contributes 0.0001).  When speaking about orders-of-magnitude, we only care about the “place” of the most-significant digit.  The notation used is

O(1,452.8701) = 1,000

which is three orders of magnitude greater than one (where one can think of O as a function that returns the order-of-magnitude of the number—see the “Computation” chapter for more on functions).  Usually, outside of certain computer science contexts, we do not explicitly write in terms of the order-of-magnitude function O, but instead in terms of the order-of-magnitude approximation it implies:

1,452.8701 ≈ 1,000

but the meaning is the same: we are only considering the order-of-magnitude of the number—usually to compare it to another number and see if they are anywhere near equivalent or otherwise very different.

        A related topic is scientific notation which makes use of exponents to more easily write numbers of very small or very large orders-of-magnitude—both of which show up very often in the sciences where we may be counting the vast number of galaxies, or measuring the very small mass of an electron.  The way it works is, one writes the number out as if its most-significant digit is in the ones place (and any others then beyond the decimal point) and then multiply it by the order-of-magnitude needed to restore it to its actual value (technically, by the number you divided it by such that the most-significant digit would be in the ones place).  One may write this using the multiplication sign and ten raised to the proper exponent, or by using “E” followed by the proper exponent.  Here is what 1,452.8701 looks like in scientific notation:

1,452.8701 = 1.4528701 × 10³ = 1.4528701E3

This works just as well for very small numbers, as well, because one may make use of negative exponents.  So for example, the number 0.0003409 is equivalent to 3.409 × 10^-4 (or 3.409E-4).

        Returning to number systems, equipped with what we just learned, we realize that the “places” in a base-10 numbers are separated by orders-of-magnitude (or by a difference of one in the exponent of the base, which is again, 10):
                10³    10²    10¹    10⁰    10^-1    10^-2    10^-3    10^-4

                 1       4       5      2       8       7       0       1
Such that the total number is (1 × 10³) + (4 × 10²) + (5 × 10¹) + (2 × 10⁰) + (8 × 10^-1) + (7 × 10^-2) + (0 × 10^-3) + (1 × 10^-4) = (1 × 1,000) + (4 × 100) + (5 × 10) + (2 × 1) + (8 × 0.1) + (7 × 0.01) + (0 × 0.001) + (1 × 0.0001) = 1,452.8701₁₀.  Now one can begin to generally see that a number system is a way of writing a quantity (like a dialect of the same language) in terms of a base, unified by the linchpin that each has a ones place (because raising any base to the 0^th power yields one), and that from there, the magnitude of each “place” is simply the base raised to progressively higher exponents (to the left) or progressively lower exponents (to the right):

… base⁵ base⁴ base³ base² base¹ base⁰ base^-1 base^-2...

One may have any number of “places” they want because we think there are infinitely many possible numbers!  While one can use any number they want as a base, some common ones, used for example in computer science, are hexadecimal (base-16), decimal (base-10), octal (base-8), and binary (base-2).  Now, what values can a given “place” take on?  We know that in decimal (base-10), each “place” may only hold one of ten values (0 through 9); this indeed generalizes, a “place” in a given number system may hold one of base values, ranging from 0 through (base - 1).  Notice that in hexadecimal, a single place must be able to hold (base - 1) = (16 -1) = 15 different values—but we only have ten single-symbolic numerals: again, 0 through 9.  How does one denote a single-symbolic 10₁₀, 11₁₀, 12₁₀, 13₁₀, 14₁₀, and 15₁₀ in number systems with bases which exceed 10?  (Note that we need the ₁₀ subscript on these because only the single-digit numerals, up to the current (base - 1) mean the same thing across number systems, as again, they all share a ones place):
                                        1₁₆ = 1₁₀ = 1₈ = 1₂
                                        5₁₆ = 5₁₀ = 5₈ = 101₂
                                        9₁₆ = 9₁₀ = 11₈ = 1001₂

For numerals whose single-symbolic values are larger than the number system's (base - 1) number of values they're allowed to hold, one needs to spread the number's symbology over several “places”, as one can see above.  You are shortly going to learn how to do that. But first, back to the question of how to denote single-symbol quantities larger than 9 in hexadecimal: by convention (and remember, all our symbolic numerals thus far have merely been Indo-Arabic convention), we use A₁₆, B₁₆, C₁₆, D₁₆, E₁₆, and F₁₆ to denote the single-symbol version of the quantities 10₁₀ through 15₁₀.  I am now going to construct a few number systems and then convert their values into our more comfortable base-10 form in the hopes of showing how they work.  Binary (base-2) is useful in computer science (for more on this, read the “Computation” chapter).  Its base numbers that each “place” (in this case, known as a bit) may hold are 0 and 1 (no other single-digit numerals are allowed).  So all numbers will look something like 100101101₂ (and, due to its application in computer science, you will rarely see a bit-point, the equivalent of a decimal point—binary is usually only used for integers).  How do we read that number? Let us break it down as before:

                            2⁸    2⁷    2⁶    2⁵    2⁴    2³    2²    2¹    2⁰

                            1     0     0    1    0     1    1    0    1

which is equivalent to:
                        256    128    64    32    16    8    4    2    1

                          1        0       0      1      0     1    1    0    1

such that you may convert this binary number into decimal as follows: 100101101₂ = (1 × 256) + (0 × 128) + (0 × 64) + (1 × 32) + (0 × 16) + (1 × 8) + (1 × 4) + (0 × 2) + (1 × 1) = 301₁₀.  Now let us try octal (sometimes used in computer science in place of binary because the base 8 is a multiple of the base 2 and so may be quickly converted to useful binary by the computer, despite being more easily read and written by humans).  Given the number 71032₈, we can write out the octal places above the values as such:
                                        8⁴    8³    8²    8¹    8⁰

                                         7    1    0     3     2

which is equivalent to:
                                    4,096    512    64    8    1

                                       7          1       0     3    2

such that one may convert this octal number into decimal as follows: 71032₈ = (7 × 4,096) + (1 × 512) + (3 × 8) + (2 × 1) = 29,210₁₀.  And finally, a hexadecimal example, which we may as well do with a fractional number (note that here, the dot is called a “hexadecimal point”, not a “decimal point”, which would imply base-10): 4B1.F₁₆.  As before:
                                        16²    16¹    16⁰    16^-1

                                          4      B      1       F

which is equivalent to:

                                        256    16     1    0.0625

                                          4       B     1         F

such that one may convert this hexadecimal number into decimal as follows: 4B1.F₁₆ = (4 × 256) + (11 × 16) + 1 + (15 × 0.0625) = 1,200.9375₁₀.

        Finally, we arrive at calculus, co-discovered by the first proper physicist, Sir Isaac Newton, and mathematician Gottfried Leibniz in the late 17^th century.^XVII  Algebra can analytically give us the areas, volumes, and general descriptions of regular shapes (and shapes who can be broken down into a summation of regular shapes), but anything more naturally curvy and irregular escapes algebra (outside of the rough estimates and averages it provides in such cases—no small feat for such an old discovery!).  Calculus is a more general theory which allows for the analytical description of irregular curved shapes and instantaneous rates, by taming infinities: fundamentally, calculus allows one to get a finite answer to an infinite sum of infinitesimal (or, infinitely small) values.  Calculus begins by thinking about limits: that is, what happens to the values of certain variables as other variables tend towards numbers like 0 or infinity (∞).  When limits are taken, variables tend towards some value, that is, they do so asymptotically (never quite reaching the value but always approaching ever-closer).  Take for example, the function, 1 / x.  What happens if x tends to infinity?  One may see by induction (testing cases), that 1 / ±1 = ±1, 1 / ±50 = ±0.2, and 1 / ±100 = ±0.01: it appears that as x tends to plus-or-minus-infinity, 1 / x tends towards zero (because division by larger numbers yields smaller quotients)!  One may think of this in the following way: 1 / ±∞ = ±ε ≈ 0 (where the Greek letter, epsilon, is the symbol for the infinitesimal—the hypothetical smallest quantity that isn't quite zero).  How about as x tends to zero (infinitesimal)?  Again, one may look at the same old tests in reverse, and perhaps add one more: 1 / ±100 = ±0.001, 1 / ±50 = ±0.2, 1 / ±1 = ±1, 1 / ±0.1 = ±10: it appears the output will keep growing forever—towards positive-or-negative-infinity (because division by ever smaller numbers yields larger and larger quotients).  One may think of this in the following way: while 1 / 0 is strictly undefined (one cannot divide by zero—that is, one cannot break an object into zero parts), 1 / ±ε = ±∞ (one can break an object into infinitely many infinitesimal portions).  To express this in terms of limits, one would write:
                                        lim_{x → ±∞} 1 / x = 0

                                        lim_{x → 0} 1 / x = ±∞

because as x asymptotically approaches plus-or-minus-infinity, 1 / x asymptotically approaches zero; conversely, as x asymptotically approaches zero, 1 / x asymptotically approaches plus-or-minus-infinity.  One can plainly see this by graphing 1 / x:^XVIII

where the top-right (or first quadrant) of the graph represents positive values for x, and the bottom-left (or third quadrant) of the graph represents negative values for x.  The “points” drawn are not actual points which are ever reached, but represent x and y values that are asymptotically approached in the limits.

        But as mentioned early on, abstract mathematics can place this finding on more rigorous deductive grounds, and to do that, we use the fundamental theorem of calculus, which analyzes what happens when we consider the instantaneous change in a function's output, given the smallest possible (ε) change in its input, at a certain point along a curve or line:^XIX

lim_{Δx → 0} Δf(x) / Δx = lim_{Δx → 0} (f(x + Δx) – f(x)) / Δx

This returns the derivative, or the slope of the straight-line tangent to that point on the curve (which is, again, the instantaneous rate of change at that exact point, in that exact direction).  In the previous example of 1 / x, taking the derivative about the points in which x is closer to zero will yield ever larger slopes as the curve ramps y up towards infinity; conversely, taking the derivative about the points in which x is larger will yield ever smaller slopes, as the curve dampens y down, tending towards zero.  Take a look at a few such lines tangent to different points on the graph (drawn in gray), and notice their different slopes (notice too, the nature of lines tangent to the curve to gain an intuitive sense of tangents):

        One may use the fundamental theorem of calculus to derive easier rules for calculating derivatives, more generally.  I will not go into them in detail, here (though I may provide some in a “Mathematical Appendix”), but suffice it to say that the most simple rule is:^XX

d/dx xⁿ = nx^n-1

where d/dx means “take the derivative of the following function (in this case, xⁿ) with respect to the variable, x” (or, find the slope of a line tangent to the original function, at position x).

        Inversely, calculus may be used to calculate infinite sums of infinitesimal contributions—integrals are calculations of the area under a curve.  One may initially think of this in terms of approximations.  One way to estimate the area under an abnormal curve is to construct a set of contiguous rectangles of varying heights such that it looks like a digital, low resolution version of the curve; then sum up said rectangles:

As you can see, there are eight hypothetical rectangles each of different heights but of the same constant width: w = 10.  We can think of those heights as a collection, each being dented by h_i where i is the current index into the collection of rectangle-heights: h₁ is the height of the first, h₂ is the height of the second, and so on.^XXI  Therefore the approximate area under the curve is the sum of the areas of these rectangles:
        A ≈ ∑wh_i = (10 × 76) + (10 × 68) + (10 × 64) + (10 × 68) +

            (10 × 71) + (10 × 77) + (10 × 80) + (10 × 80) = 5.840 units²
(where, as you can see, the Greek sigma means “summing over a collection”, in this case, a collection of areas, or the sum of the products of a constant width with a collection of heights).  How might we take this blunt approximation (just look at the details of the curve that are left out by looking at it as a sort of bar-graph of rectangles) and make it more precise?  Well, we could double the number of rectangles used to 16 (each with half the width, w = 5), thereby doubling the number of heights (which increases the sensitivity of the estimate of the curve).  The beauty of integral calculus is that it allows us to take this idea to its logical extent: imagine infinitely many rectangles, each of infinitesimal width (w = ε) and now infinitely many heights which make this method perfectly sensitive to the curve: by definition, it is the curve.  This is what taking the definite integral of a region of a curve does, providing the analytical (as opposed to the approximate) answer for the area under the curve.  Because integration is the inverse of derivation (and vice versa), the general rule for integration is:^XXII

∫xⁿ dx = xⁿ⁺¹ / (n + 1) + c

(where c is any constant, because this value is irrelevant to the process).  While these tools and others may be used to derive rules for performing derivations given more complex functions, we will take some of them for granted, here.  Let's take the actual function drawing the curve above to be:

f(x) = 10cos(x / 15 + 1) + 74.5

The integral is then calculated thus:^XXIII

    ∫f(x) dx = ∫10cos(x / 15 + 1) + 74.5 dx

    Coefficients may be un-distributed to the outside of the integration;

    the integral of the sum is the sum of the integrals

    10∫cos(x / 15 + 1) dx + ∫74.5 dx

    The integral of a constant is the product of that constant and the variable

    10∫cos(x / 15 + 1) dx + 74.5x

    Substitution: the integral of a nested function, f(u(x)), is the product of the

    integral of the outer function with respect to the inner function, and the integral

    of the inner function with respect to the variable of interest
    u = x / 15 + 1

    10∫cos(x / 15 + 1) dx + 74.5x = 10∫cos(u) du × ∫x / 15 + 1 dx + 74.5x

    The integral of cos is sin; and the integral of the sum is the sum of the integrals

    10 × sin(u) × (∫x / 15 dx + ∫1 dx) + 74.5x

    The integral of a constant is the product of that constant and the variable

    10sin(u) × (∫x / 15 dx + x) + 74.5x

    Coefficients may be un-distributed to the outside of the integration

    10sin(u) × ((1/15)∫x dx + x) + 74.5x

    ∫x¹ dx = x¹⁺¹ / (1 + 1) = x² / 2

    10sin(u) × ((1/15) × (x² / 2) + x) + 74.5x

    10sin(u) × (x² / 30 + x) + 74.5x

    Substitute u = x / 15 + 1 back in for the final answer

    10sin(x / 15 + 1) × (x² / 30 + x) + 74.5x

Now, we may take the definite integral over the domain of x = 0 through 85 to get the area under the curve in our image:

    ∫₀⁸⁵10cos(x / 15 + 1) + 74.5 dx = |₀⁸⁵10sin(x / 15 + 1) × (x² / 30 + x) + 74.5x =

    The definite integral is the difference between the integral as evaluated

    substituting both bounds in as the variable

    10sin(85 / 15 + 1) × (85² / 30 + 85) + 74.5 × 85 -

    10sin(0 / 15 + 1) × (0² / 30 + 0) + 74.5 × 0

    10sin(5.667 + 1) × (7,225 / 30 + 85) + 6,332.5 - 10sin(1) × 0 + 0

    10sin(6.667) × (240.8 + 85) + 6,332.5

    10 × 0.3745 × 325.8 + 6,333

    3.745 × 325.8 + 6,333

    1,219 + 6,333

    7,552

〰〰

    Now, I want to remind you again of what I said at the beginning of this chapter: do not be afraid!  This chapter was meant to introduce you to the philosophy of mathematics, some of the basic elements of mathematics, and to serve as an early reference book and toolbox as you explore your own problems in the future.  Nobel-Prize-winning physicist Richard Feynman warned against other physicists' “precious mathematics”: one should be searching for the most elegant (not complicated or fancy) explanation for one's phenomenon of study, and that includes its mathematical description (or the degree to which one even uses math).^XXIV  In principle, mathematical description must always be possible, but in practice it is often not available.  While some work has been done to understand the mathematics at play, naturalist Charles Darwin's theory of evolution by natural selection was largely a work of philosophy of biology: hypothesized, empirically verified, and now forming the foundation of the entire field of biology all without math playing a particularly integral role.  On the other hand, physicist Albert Einstein's general theory of relativity was crucially derived and described in precise (and complex) mathematical terms before being empirically confirmed.  Entomologist E. O. Wilson shares these sentiments, and points out that while a scientist really ought to be familiar and comfortable with at least the basics of mathematics, he may partner up with someone more mathematically inclined if their line of inquiry requires such a thing.^XXV  It is certainly not the case that all scientists are mathematical wizards (the lower-level the science, the more math is necessary, in general; though, for the industrious among us looking to make a contribution, this also often means that the lower-level sciences could use more philosophical work and the higher-level sciences could use more mathematization).

        Philosophy of mathematics is where thinkers argue over what math really means, in what sense it is real or true.  Is it merely a tool?  A language?  Some, like computational physicist Max Tegmark, glimpse the future unification of mathematics and physics.  I think this will occur, in the final analysis.  But for now, the disciplines remain too far apart, the use of one as the language of the other is the current depth of their relationship.  Whereas Tegmark argues for a naive mathematization of physics with his level IV multiverse or mathematical universe hypothesis (in which all legal mathematical structures get their own instantiation or manifestation, each a real, physical universe)^XXVI, I believe that when they meet somewhere in-between, it will be truer to say that mathematics was physicalized.  This means that the fundamental axioms of logic and mathematics will prove to be physically manifest—something we can confirm through empirical induction, and with which all of math and physics may ultimately be derived.  At the risk of naivete, I ask you to imagine something like the basic law that:

A ≠ !A

may have a physical correlate at the bottom of everything: perhaps the fact that no two objects may inhabit the same exact position in space-time, or otherwise that the same object may not exist in multiple positions in space-time but must be in one, or simply that a physical object is that object and not another.  Perhaps something like this is true for all fundamental axioms.  It may be that a full understanding of mathematics limits its axioms and derivations to those of physical reality.  In any event, one can already see the consequences of the laws of logic emergent in nature: the process of evolution by natural selection is essentially a trial-and-error process-of-elimination—the (necessarily) backward-looking, and forward-predicting process of induction being “used” to create fecund creatures (for more on this process, see the “Biology” chapter).

        This idea is related to the physicists' quest for a theory of everything: they have been attempting to work towards a fundamental quantum physics which will be able to deduce not only physical laws, but physical constants, from first principles (keeping in mind that to check if this is the right deductive system, empirical evidence would still be needed to confirm the predictions against the real world).^XXVII  While I'm sympathetic to the view that something like this will ultimately prove true, I think that such researchers get ahead of themselves: a (in some ways less, in some ways more ambitious) theory of everything (something more like what physicists call a grand unified theory) which mechanically accounts for all forces at once, despite “unexplained” and empirically measured physical constants would be an achievement leaps and bounds beyond the current state of the field, even without explaining exactly why this unified theory (and its constants) and not some other.^XXVIII

        As you can see, mathematics provides for philosophers a rigid body of deductive truth with which to articulate their best ideas with precision.

Footnotes:

0. The Philosophy Of Science table of contents can be found, here (footnotephysicist.blogspot.com/2022/04/table-of-contents-philosophy-of-science.html).

I. I retrieved this quotation from MacTutor's “Quotations: Galielo Galilei” web-page (University Of St. Andrews, Scotland) (https://mathshistory.st-andrews.ac.uk/Biographies/Galileo/quotations/#:~:text=%5BThe%20universe%5D%20cannot%20be%20read,to%20comprehend%20a%20single%20word.) and the publication date from the Wikipedia entry “The Assayer” (Wikipedia) (retrieved 4/29/2022) (https://en.wikipedia.org/wiki/The_Assayer) (although I have neither fully read Galilei's work nor these web pages).

II. I cannot seem to remember the textbook used in the Physics I and II courses I took at Rutgers University Camden, but I believe this is where I first read about this, and in most detail.

III. It is sometimes claimed that there technically exist “unitless” / “dimensionless” ratios which hold physical meaning, such as the ratio of the masses of the electron and proton: as long as the units of the mass of the two particles are the same, whatever their magnitudes, that ratio will remain constant. But even this cannot escape units entirely, because technically, ratios and the use of units are one in the same: a unit is describing one object in terms of the other—the definition of a ratio (in the previous example, the “dimensionless ratio” of the proton's mass to the electron's mass is technically just setting the electron's mass to 1 electron-mass and then using the electron-mass as the unit for the magnitude of the larger proton mass). Abstract mathematics comes closer with constants such as pi (the ratio of a circle's circumference to its diameter is always π ≈ 3.14, see “Pi (π)”, MathIsFun, https://www.mathsisfun.com/numbers/pi.html; though I have not read this full page), but even this is technically an expression of this circle's circumference with the use of its arc-length as the unit (with the important feature that doing so yields the same magnitude for any sized circle). Poet Nick Montfort even seems to claim that a number in and of itself is purely abstract and unitless (though he may have simply meant that numbers need not only or always be used to describe spatial lengths), see Exploratory Programming For The Arts And Humanities by Nick Montfort (MIT Press) (2016) (pp. 147), but even this is somewhat misleading: the number “five” means “five ones” in a sort of degenerative case of abstract quantitative “units” (this exercise becomes less obtuse when we realize that we do this explicitly in our number systems, depending on the base, which will be described later in this chapter: with everyday base-ten numbers, we know that the “2” in “25” doesn't mean two but “two tens” or twenty). It is important to understand quantities in the abstract (indeed, there exist exotic quantities such as “imaginary numbers” which defy simple understanding), but all of mathematics is about logical relationships at base (relationships which gain much meaning once the world is understood through their marriage with physical units), see Our Mathematical Universe by Tegmark (at least pp. 260-271).

IV. The Pythagoreans took great issue with their discovery that the square root of two (√2), something we will explore later in this chapter, could not be expressed as a ratio of whole numbers, see Cosmos by Sagan (pp. 195).

V. I struggled to find where I had originally read about this, but can source it to “History & Background” by Tyson Larsen (Utah State University) (http://5010.mathed.usu.edu/Fall2015/TLarsen/History.html#:~:text=1637%3A%20Rene%20Descartes%2C%20a%20renowned,as%20being%20fictitious%20or%20useless) (though I have not read this full page, and it now appears unavailable). This is not all that uncommon: another example is the big bang theory from Cosmology. It is the accepted theory for the origins of the universe, today, but the main proponent of an alternative in the 20^th century (the steady state model), cosmologist Sir Fred Hoyle, originally coined “The Big Bang” as a derogatory term on a radio show!

VI. Keep in mind that while the = symbol means value-equivalence, the ≡ symbol means expression-equivalence (stating that two value-equations are equivalent expressions, or isomorphic).

VII. See "Infinity" by Max Tegmark (Edge / Harper Perennial) (2014 / 2015) (https://www.edge.org/response-detail/25344) from This Idea Must Die edited by Brockman (at least pp. 48-51) and Our Mathematical Universe by Tegmark (pp. 313, 316-317).

VIII. See "Infinity" by Tegmark (https://www.edge.org/response-detail/25344) from This Idea Must Die edited by Brockman (at least pp. 48-51) and Our Mathematical Universe by Tegmark (pp. 313, 316-317).

IX. My father tells a story about one of his teachers explaining multiplication in just this way, a story which clearly stuck with him since his youth.

X. I will tend to use the symbol × to denote the multiplication operation, but elsewhere, one will often see an x, •, or * as well. Note that in matrix mathematics, above the level of basic arithmetic, the dot-product and cross-product of two such matrices (a special kind of collection of numbers) are actually different operations. It is also the case that two touching parenthetical quantities (in this following examples, binomials) denotes distributive multiplication, as in:

            (1 + 1)(2 + 2) = (1 × 2) + (1 × 2) + (1 × 2) + (1 × 2) = 2 + 2 + 2 + 2 = 8.

Similarly, if a naked number is affixed to the front of a variable or parenthetical, this also calls for multiplication: 5r means “five times r” and 7(1 + 1) = 7 × 2 = 14.

XI. See the “Definition Of Divisor” page on MathIsFun (https://www.mathsisfun.com/definitions/divisor.html#:~:text=The%20number%20we%20divide%20by.&text=Example%3A%20in%2012%20%C3%B7%203,integer%20exactly%20(no%20remainder).

XII. See the Google equations entry for the volume of a rectangular pyrimid (https://www.google.com/search?q=volume+of+a+pyrmid&rlz=1C1CHBF_enUS775US775&oq=volume+of+a+pyrmid&aqs=chrome..69i57j0i10l9.8272j0j4&sourceid=chrome&ie=UTF-8) and of a cylinder (https://www.google.com/search?q=volume+of+a+cylinder&rlz=1C1CHBF_enUS775US775&sxsrf=ALeKk03rqjUbPzHOR-YlfP7gYeQXEDNYPA%3A1627189885917&ei=ffL8YLO3N6Gw5NoP45yikAY&oq=volume+of+a+cylinder&gs_lcp=Cgdnd3Mtd2l6EAMyAggAMgIIADICCAAyAggAMgIIADICCAAyBwgAEIcCEBQyAggAMgIIADICCAA6BwgAEEcQsAM6BwgAELADEEM6BQgAEJECSgQIQRgAUIBoWNBvYJxwaAJwAngAgAFkiAGSBJIBAzguMZgBAKABAaoBB2d3cy13aXrIAQrAAQE&sclient=gws-wiz&ved=0ahUKEwjz6YbZuv3xAhUhGFkFHWOOCGIQ4dUDCA8&uact=5).

XIII. Mathematician David Mumford claims that pre-Greek cultures, such as “... the Babylonians, Vedic, Indians, and Chinese...” were familiar with the theorem, see “Was Pythagoras the First to Discover Pythagoras’s Theorem?” by Anna Barry (University Of Minnesota / SIAM News) (https://www.ima.umn.edu/press-room/mumford-and-pythagoras-theorem) (though this article no longer seems to be available). At odds, historian of philosophy Anthony Gottlieb claims the theorem “... belong[s] to the middle of the fifth century BC or later, long after the death of Pythagoras,” see The Dream Of Reason: A History Of Philosophy From The Greeks To The Renaissance by Anthony Gottlieb (W. W. Norton & Company) (2000 / 2016) (pp. 40).

XIV. See the “Inverse Sine, Cosine, Tangent” page on MathIsFun (https://www.mathsisfun.com/algebra/trig-inverse-sin-cos-tan.html) (though I did not read this entire entry for the purposes of this citation).

XV. See the “Polar and Cartesian Coordinates” entry on MathIsFun (https://www.mathsisfun.com/polar-cartesian-coordinates.html) (though I did not read this entire entry for the purposes of this citation), which includes both the equations I present, as well as the conceptual basis for my diagram.

XVI. Here, the subscript denotes the base of the number system in use. 10 is explicitly used in this context because we are talking about number systems, but in most contexts, when you see a number without such a subscript, base-10 is the implicit assumption.

XVII. See “Gottfried Wilhelm Leibniz” by Richard S. Westfall (Encyclopaedia Britannica) (1998 / 2021) (https://www.britannica.com/biography/Gottfried-Wilhelm-Leibniz) and “Isaac Newton” by Richard S. Westfall (Encyclopaedia Britannica) (1999 / 2022) (https://www.britannica.com/biography/Isaac-Newton) (note that I have not read either article in full).

XVIII. I used the online graphing calculator, Demos to assist me with figuring out the general shapes for diagrams (https://www.desmos.com/calculator).

XIX. See The Theoretical Minimum: What You Need To Know To Start Doing Physics by Leonard Susskind and George Hrabovsky (Basic Books) (2013) (pp. 29-30) (note that I have not yet finished this book). Note that the Greek letter, delta (Δ), here denotes a change in a variable. For example, if you have an initial position, x, and a final position x', then the change in position Δx = x' – x. Furthermore, the function notation f(x) means that x is being passed into a function named f for output to be returned, which will be discussed further in the “Computation” chapter.

XX. See The Theoretical Minimum by Susskind and Hrabovsky (pp. 32-34).

XXI. For more on collections and arrays, see the “Computation” chapter.

XXII. See The Theoretical Minimum by Susskind and Hrabovsky (pp. 52-53). Note that the squiggly integration symbol, ∫, is actually an “S” for “sum” (in the case of calculus, an infinite sum).

XXIII. See The Theoretical Minimum by Susskind and Hrabovsky (pp. 54).

XXIV. "A Centennial Celebration For Richard Feynman" by Whitney Clavin (Caltech) (2018) (https://pma.caltech.edu/news/centennial-celebration-richard-feynman-82264) (though I have not read this full article); "Dick's Tricks" by Leonard Susskind (Caltech) (2018) (https://www.youtube.com/watch?v=ldfUAzRMs_k) (21:46-22:46); and "Feynman-'what differs physics from mathematics'" uploaded by YouTube user PankaZz (https://www.youtube.com/watch?v=B-eh2SD54fM).

XXV. "See the "Mathematics" chapter from Letters To A Young Scientist by Edward O. Wilson (Liveright Publishing Corporation) (2013) (pp. 27-41) and "Advice To Young Scientists - Edward O. Wilson" by E. O. Wilson (Ted-Ed) (2013) (https://www.youtube.com/watch?v=ptJg2GScPEQ) (3:48 – 9:03).

XXVI. See Our Mathematical Universe by Tegmark (pp. 267, 318-319, 321-325, 335-336, 350-357, 363) and "The Universe" by Seth Lloyd (Edge / Harper Perennial) (2014 / 2015) (https://www.edge.org/response-detail/25449) from This Idea Must Die edited by Brockman (pp. 11-14).

XXVII. For more on this topic, see the “Empiricism” chapter.

XXVIII. See “In Defense Of Philosophy (Of Science)” by Gussman (footnote 22) (https://footnotephysicist.blogspot.com/2021/05/in-defense-of-philosophy-of-science.html) which further cites “A Profusion Of Place | Part I: Of Unity And Philosophy” by Steven Gussman (Footnote Physicist) (2020) (https://footnotephysicist.blogspot.com/2020/03/a-profusion-of-place-part-i-of-unity.html).